Worksheet: MOA-2009-BLG-266L

by Jennifer Yee (SAO), Sydney Anderson (Swarthmore), Linda Vu (Swarthmore)

Gaudi & Gould (1997) showed that the parameters of a planet (s and q) can be approximated analytically based on light curve observables.




Microlensing Event: MOA-2009-BLG-266L

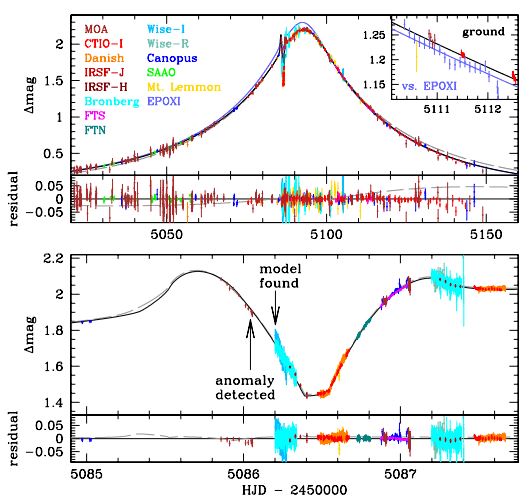
Lightcurve of MOA-2009-BLG-266

Lightcurve of MOA-2009-BLG-226L


Muraki et al.(2011)



Parameters of the Underlying Stellar Event

Based on the microlensing light curve, figure out the following properties of the microlensing event:

Your answers
Time of the peak of the event = t0:
Change in magnitude = Δm:
Maximum magnification = Amax:
Impact parameter = |u0|:
Magnitude at Half-Maximum =
Full Width Half Maximum = tFWHM:
Einstein Timescale = tE:








Parameters of the Planetary Event

1. Where is the planet?

Your answers
Time of the the planet perturbation = tplanet :
Time scaled to the Einstein timescale = τ = |tplanet - t0|/tE :
Source-lens separation = u = √(u02 + τ2) :
y± = ± (½) (√(u2 + 4) ± u) :
Is the perturbation a major image (+) or minor image (-) perturbation?
Location of the planet = s :









2. What is the mass ratio between the planet and the star?

Your answers
Planet Einstein Timescale = tp,E ~ tFWHM :
Mass Ratio = q = (tp,E / tE)2:





Planet      q = Planet Mass/Sun's Mass 
   Jupiter      10-3 
   Neptune      5 x 10-5 
   Earth      3x 10-6 
Your answer
Is the planet more similar to Earth, Neptune, or Jupiter?

How well did you do?

1. We're astronomers, so if you're right within a factor of a few, that's pretty good.
2. The approximation works less well as s--> 1
3. IF the light curve is in magnitudes (rather than magnification): We're assuming zero blending, i.e. that all the light that you see is from the source star. If there is some other (non-lensed) light blended with the light curve, then the true magnification is higher. How do your answers change if you assume that half of the baseline flux is due to a blend? What if 90% is due to a blend? Hint: Δm = -2.5 log10 [(A*fs+fblend)/(fs+fblend)]

You can also view the original paper: Muraki et al. 2011 ApJ 741, 22

References:

Gaudi, B.S. & Gould, A. (1997), ApJ, 486, 85
Muraki, Y. et al. (2011), ApJ, 741, 22