by Jennifer Yee
In microlensing, the caustic corresponds to the position(s) of the source for which the solution of the lens equation results in infinite magnification. For a point lens (e.g. a single star), the magnification equation is:
| Magnification = | A(u) = | u2 + 2 |
| u (u2 + 4 )1/2 |
where u is the source positions. If you solve this equation for u=0, you will find that the magnification, A, is infinite. Thus, for a point lens, the caustic is a single point at u=0.
For a 2-body lens (such as a star+planet), the magnification equation is more complex, but it remains true that there are solutions to this equation for which the magnification is infinite. In this case, the caustic is a closed curve, or set of closed curves, and at those curves the magnification diverges to infinity.
By solving the lens equation, it is possible to calculate the magnification of the source at any (projected) position relative to the position of the lens. The magnification map is a visualization reflecting the calculated magnification at a given point (brighter=more highly magnified). The image below shows the magnification map and caustic structure for a 2-body lens.
| Magnification Map | Caustic | Magnifcation Map & Caustic |
|
Magnification mapJennifer Yee |
CausticJennifer Yee |
Magnification map and causticJennifer Yee |
Some general rules about caustics:
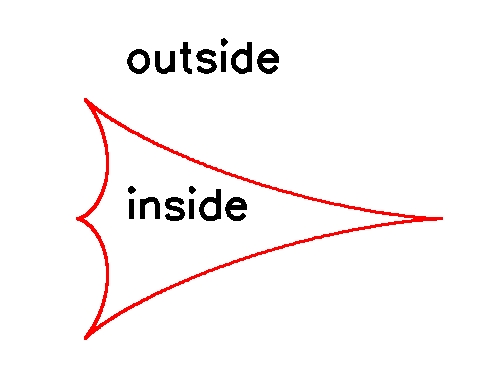
They are closed curves. Therefore, they have an inside and an outside. (The perimeter of a square or a triangle are other examples of closed curves. But remember that the caustic refers to the edge of the shape and not the shape itself.)
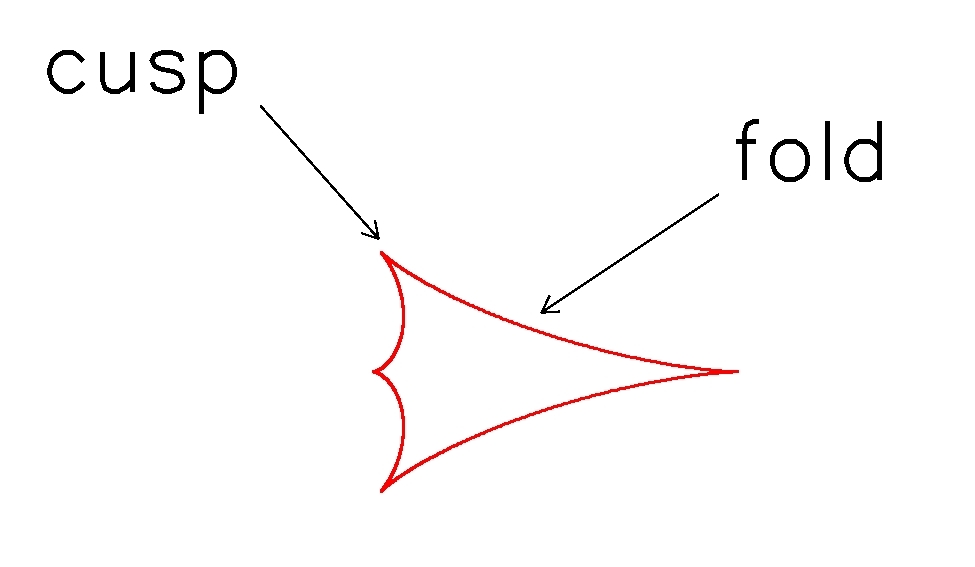
The points of a caustic are called cusps. The curved segments connecting the cusps are called folds.