
by Jennifer Yee
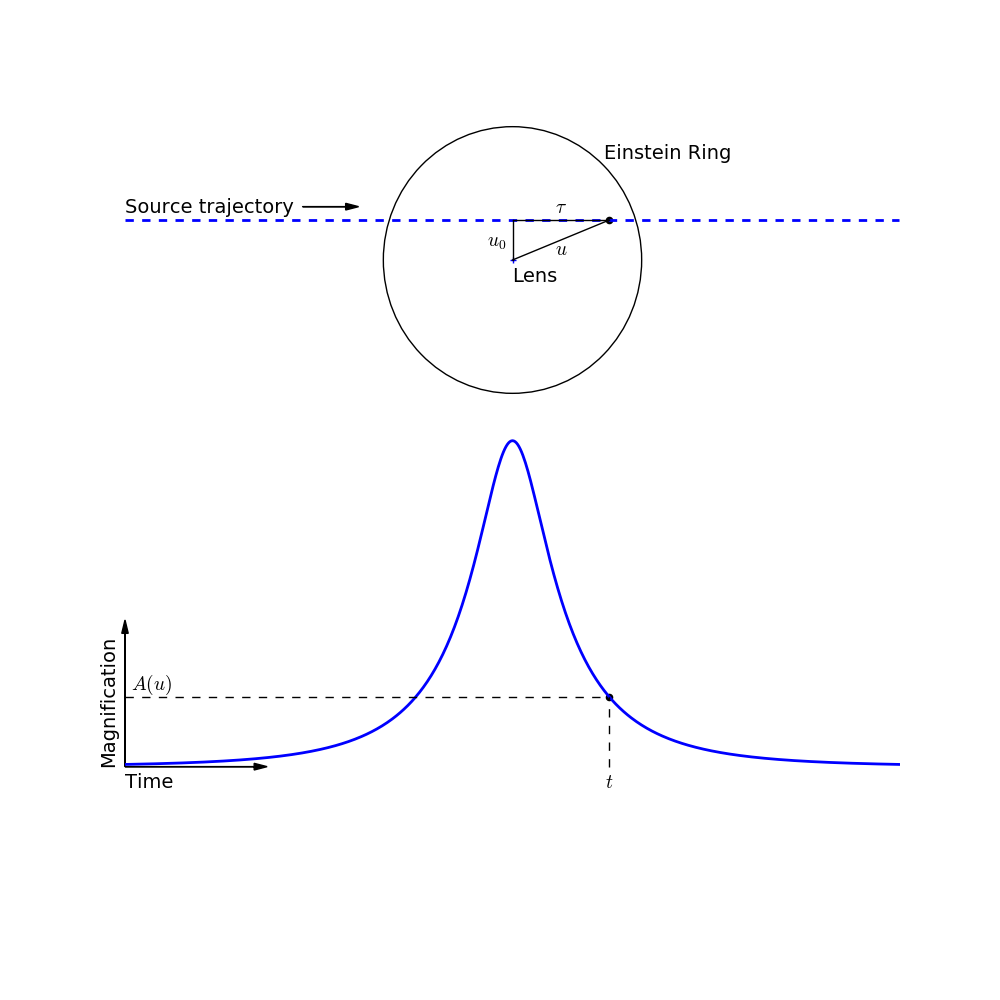
A point lens microlensing event is parameterized by three variables:
The magnification of the source is given by the equation:
| Magnification = | A(u) = | u2 + 2 |
| u (u2 + 4 )1/2 |
where
and
| τ = | (t - t0) |
| tE |
Below are discovery lightcurves of the first microlensing events. For each one, estimate its point lens parameters (t0, u0, tE). These basic parameters can be directly inferred from the lightcurve by measuring the height and time of the peak and tFWHM of the lightcurve (FWHM = Full Width Half Maximum). Then, tE can be calculated using the measured tFWHM and the above equations. In the limit where u0 << 1, tE ~ (1/2)tFWHM/u0.
|
Estimating t0 and u0 for a point source, point lens eventJ. Yee |
Estimating tE for a point source, point lens eventJ. Yee |
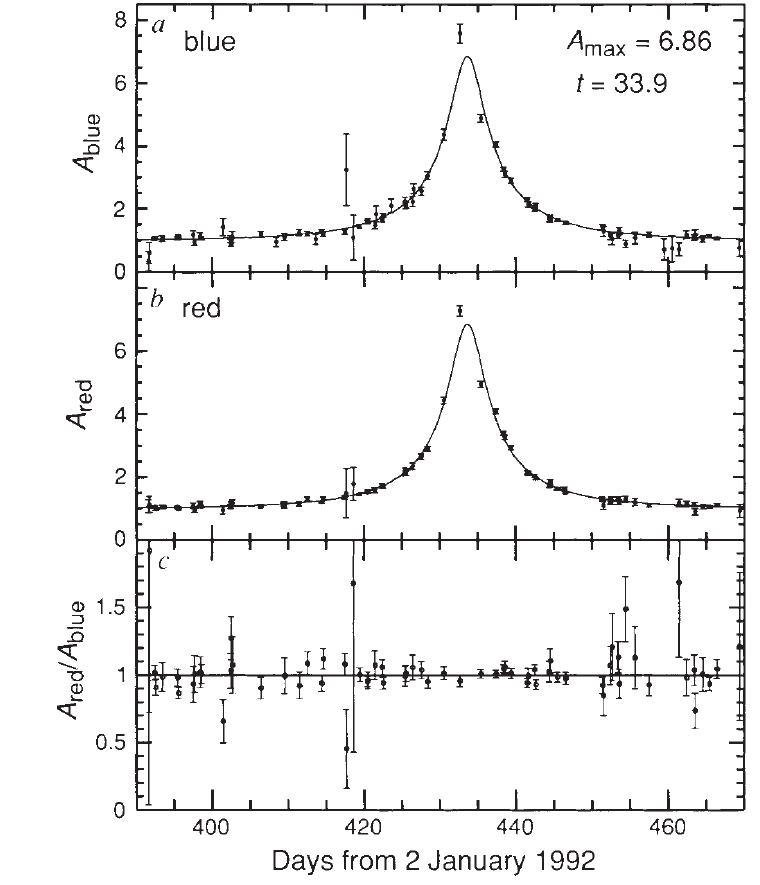
| Your answers | ||
|---|---|---|
| t0: | ||
| u0: | ||
| tE: |
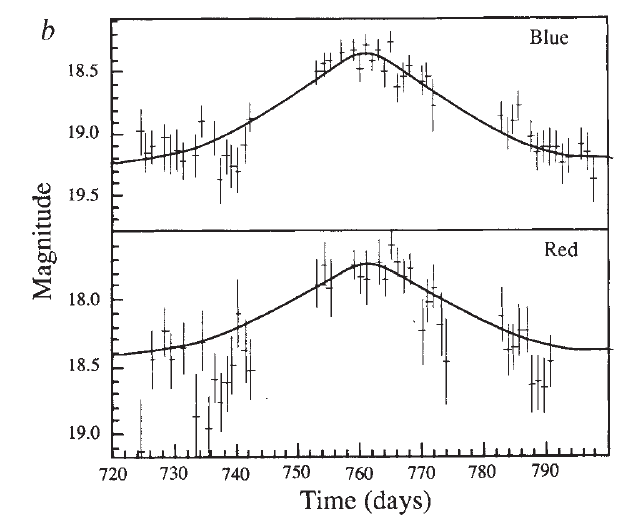
| Your answers | ||
|---|---|---|
| t0: | ||
| u0: | ||
| tE: |
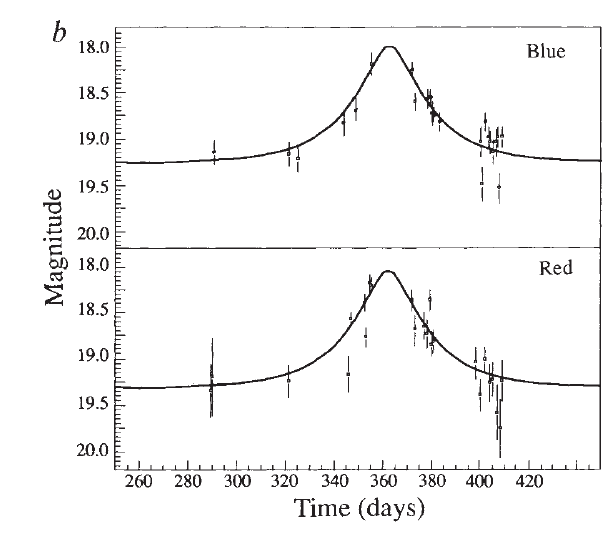
| Your answers | ||
|---|---|---|
| t0: | ||
| u0: | ||
| tE: |