Worksheet: MOA-2010-BLG-353L

Gaudi & Gould (1997) showed that the parameters of a planet (s and q) can be approximated analytically based on light curve observables.

Microlensing Event: MOA-2010-BLG-353L

Lightcurve of MOA-2010-BLG-353L(full)

Rattenbury et al.(2015)

Lightcurve of MOA-2010-BLG-353L

Rattenbury et al.(2015)

Parameters of the Underlying Stellar Event

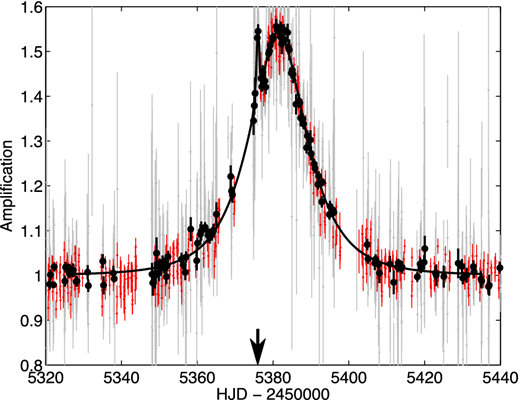
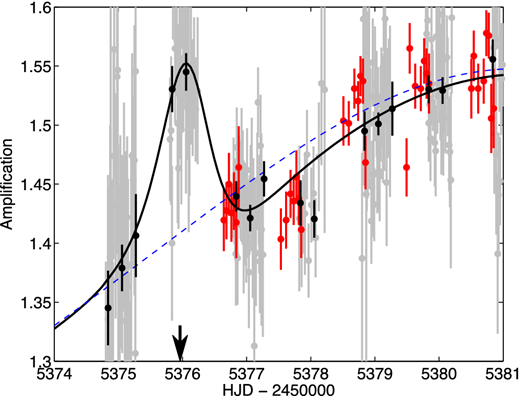
Based on the microlensing light curve, figure out the following properties of the microlensing event:

	Your answers
Time of the peak of the event = t0:
Change in magnitude = Δm:
Maximum magnification = Amax:
Impact parameter = |u0|:
Magnitude at Half-Maximum =
Full Width Half Maximum = tFWHM:
Einstein Timescale = tE:

Check
Hint

Hint 2

Hint 3

Parameters of the Planetary Event

1. Where is the planet?

	Your answers
Time of the the planet perturbation = tplanet :
Time scaled to the Einstein timescale = τ = |tplanet - t0|/tE :
Source-lens separation = u = √(u02 + τ2) :
y± = ± (½) (√(u2 + 4) ± u) :
Is the perturbation a major image (+) or minor image (-) perturbation?
Location of the planet = s :

Check
Hint 1

Hint 2

2. What is the mass ratio between the planet and the star?

	Your answers
Planet Einstein Timescale = tp,E ~ tFWHM :
Mass Ratio = q = (tp,E / tE)2:

Check Hint

Planet	q = Planet Mass/Sun's Mass
Jupiter	10-3
Neptune	5 x 10-5
Earth	3x 10-6

	Your answer
Is the planet more similar to Earth, Neptune, or Jupiter?

Check

---

How well did you do?

1. We're astronomers, so if you're right within a factor of a few, that's pretty good.
2. The approximation works less well as s--> 1
3. IF the light curve is in magnitudes (rather than magnification): We're assuming zero blending, i.e. that all the light that you see is from the source star. If there is some other (non-lensed) light blended with the light curve, then the true magnification is higher. How do your answers change if you assume that half of the baseline flux is due to a blend? What if 90% is due to a blend? Hint: Δm = -2.5 log10 [(A*f_s+f_blend)/(f_s+f_blend)]

You can also view the original paper: Rattenbury et al. 2015 MNRAS 454, 946

---

References:

Gaudi, B.S. & Gould, A. (1997), ApJ, 486, 85
Rattenbury, N. et al. (2015), MNRAS, 454, 946